N Jfbk U

Equivalence Rationnelle Et Homologie De Hochschild Pour Certaines

Prezentaciya Sostav I Ustrojstvo Kompyutera Shoe

Calameo Rev Cartes Estudio De Caso Area Musical Tarea 2
Nearsoft Grand Opening Party O09i Oae Xfvrou E U Lz Av Flickr

Panasonic Tx50dx700e Tx40dx700e Tx58dx700e Operating Instructions Manualzz

Glosario
õ þ þ ø ò ñ û ï í ú õ ö õ û î ò ú õ ø õ î û ñ ø õ þ ü û ø ô û ï í ú õ ï ú ò ÷ û ù ù ò ý ò þ ÷ õ ÷ í ô í ú í ï ÷ í ò þ ÿ ï ò õ þ ÿ û ú õ ÷ í õ û î ø í ñ í ÿ ò ø í ï ÿ û ý þ ÷ û ð û ü ý í ï í õ ÿ û ü ý õ ÿ û ù õ ø õ þ ø ð õ ü û ø ô û ï í ÿ ò ø ò ö ü ò ý ò ü ý û ñ í.

N jfbk u. Lösungsskizzen der Klausur zur Linearen Algebra im Herbst 15 Aufgabe I1 Essei(G;. } 6 ~ ^0 1 b Ë î « _ v ^ W Z 8 &0 1 É ß ¢ Û Ñ å ¢ b ö &O Û j 6WHS. @ J Á " * G I U ª æ * > $ 01 Ç §>& ¾ w>' û Ñ ( (= ( ( /=0 ô 7 £ w ( 4=9 "& £ (Ö b w Ñ * 25 § s ^ m#ë 4(' V#ã w#ã w û 90& A ô 7 £ w.
± %4 @ Ûb Û Æ /9 A µ f jM %4 Æb ²Zb9× / 0¼ eK 2° · ¥'¼b q_ u \\v_ 6ä &M ^b È q · / "I_ Ûlb X G0¼ eK 4 2°1  ¢ßîÂÝíѼî 9× /0¼ e'¼b µ. ¢ ñ ½ È µ å È é ¨ Õ ñ ¤,2 ¥ g ¤ ª ¤ r ç U F Ö » ° ¥ à Æ ë · O$ ä à Æ ë · O% Ð ¢ ñ ½ È µ å È é23(1 µ è ¸ ç ñ « ñ ® ¤,$ ,% û ¥ ¦ O% y 9 Ï V o ° r ç ¸ Ö ,%23 r Û ¢ ñ Æ b j } È µ å È é ¤1$ ¥ Ù ¤ ª à Æ . J=1 1 (j 1)2 l=1 1 (l 2)2 = 1 (1 1)2 1 (n 2)2!.
_3Æ 8"g  *ñ Z Z 8 A S 8 \ î W Z 8 r M Û Ñ b B õ _ î S K Z 8 ' ,,e  I Û Ñ b' c º v b 6 u _ G v K !ñ _ E 8 S u È ( µ r O S Ì î à î b V _ O Z í¶ Ü 'ö K S * %@ } O Z > A >1 v 6 u _*ç q µ T u Ï µ º _ ° Z' Ü < c Ó b0¼ \ \ v _ Ü < \ M ¼. U Z 8 r M = ¥. Go To « á ñ Ø ñ Ä À Û ñ E è Ü É ã é ) î ß é I N yURL V STAY NAVI y Ø ¶ v ¹ · b d } ë ® ¢ ñ j Ú v ¢ è b d } Û ñ E è d j v z Æ ´ y ß é Ç ê · y L ç U ( O O j b d } 9 vSTAY NAVI v L ç C y O z ß é Ç ê · s Ï · í Ç Ø.
"Û ñ ¸ ½ m q ´ Ò ï « è * µ Ë k ª q q ± = n Ö h ½ Ë ª q q ± = l Õ Ö e h ½ Ë ª q q ± = s Õ Ö e h ½ Ë ª q q ± = h ½ Ë ª q q ± = m ø ñ ¸ q q ± = ½ Ë Ö ¼ q m ² Ö ª ï õ b ° c ï ï ¶ ê ö ¹ ¨ ¯ o ¾ é ¯ o ¾ m ² é ® Á n Á Ò ã 9 ¾ p Ù ¸ n ó ¸ m ² q q ± = Ù é ¯ o ¾ m ² Ù é ® Á n Á Ò ã 9 ¾ p Ù. } Û j É ß ¢ Û Ñ å ¢&É >/>3 ¡>&>2 ¡>' Û Ç « Ý ¹ Ñ î 6 í p(í Õ ¥ î « b Æ É ß ¢ Û Ñ å ¢ @ r W S C 6 u Z b ¥ E b0«) Æ \ ^ W Z > ~ r M 0«) Æ >2 X b « ¸ µ É _ ( E G \ ` I s _ Û*f 4 u Z 8 A r M Ê v ¥ E É ß ¢ Û Ñ å ¢ ¶ î Ý >&6FUDWFK>' Q W Z Û j 6WHS C ?. ) { ÛF ¦ ` ÅLÀ;ÿ ¶ ð x = j ê ,´ ú Y0 ö ÛDÛ j 0#n ¼L Ø6ü Ã ® > & { Ã 0 G JBL ® *O(,´Gý ½ u » k@ >C¥ Q7 {L$,´ t O õ0¦1 _O _ w ÛF Ë 9 µ 0 5 à { Ä< à Å,´ *AÞ.
U s / t i è Q j v C u > I y Û ¢ ñ Æ v o O q ¸ ~ d } s ó ³ Q s / l v p Z / } ª y Û ¢ ñ Æ s / l y b O i t s / t i Ï y { Æ ô s ó ³ Q s / l v U \ @ ð Á y Û ¢ ñ Æ @ Î v C u s / t i y Û ¢ ñ Æ / } ª y b O £ O s I N Î y Û ¢ ñ. Die zudem f ur p= 2 die CauchySchwarzUngleichung jhx;yij. KARLSRUHER INSTITUT FUR TECHNOLOGIE¨ Lehrstuhl f¨ur Okonometrie und Statistik¨ S T A T I S T I K II L¨osungsbl ¨atter zu den Ubungen¨ Wintersemester 13/14.
L ç v M j Õ ç · Û ¢ ñ Æ s ½ W Ü v L ç b j s ½ Ú E ¤ ß é Ç ê · A ë l ú d } ¥ r u z Õ ç · Û ¢ ñ Æ s ½ v ³ ¢ Æ u r y L ç ê & s b j HE ³ ¢ Æ y ¹ · Î L ç î Î s ½ Ú E y ç E v ~ Í ÿ Î ¤ z ³ ¢ Æ r y DX ,' ë ® ¢ ñ Î z r Õ ç · Û ¢ ñ Æ s ½ y ñ ¯ Æ Ú E u )  v û ö b d } r u z Õ ç · Û ¢ ñ Æ s ½ V O \ j �. ¤ ¥ 2 ê è ¦ µ å ñ v ~ 2 ¬ > I1'5 ¤ Ù · Á q à ¥ y ª ¢ ¾ ñ · v n q ä  d ^ s } KWWSV ZZZ GQU VWDWH PQ XV FRYLG KWPO 2 r z J 5 9 I r y D W F õ } ¤ ¥ W n s z & u Ï Ä ¡ y j. A−1 ist also das eindeutige Element mit a−1a = aa−1 = e Es gilt (a−1)−1 = a fur¨ jedes a∈ G, da aa−1 = a−1a= e, und (ab)−1 = b.
è µ y ° Z Ô È 0 ?ç>"=Û ñ ÿ û à ñ ÿ w æ ° w Ï R p Ï Ú Ö Ó µ t æ Z!. Längen und VolumenausdehnungsKoeffizienten von verschiedenen Werkstoffen wie Stahl, Kupfer, Kunststoff, Aluminium und Flüssigkeiten in Abhängigkeit von der Temperatur. # * J$17,%2',(6 &ROOHFWLYH * G J 4 ¥ b T 4 v C ã Ö Û Ñ É & ¡ 4 a i u ² µ ) ( Ä & ð ± K ¬ z · Q;.
U È È ® è · ì U 9 I1/*, ç · Û ñ Õ 9 I C \ ³ < 9 I m Ê W v þ 2 ù = Î à ¿ ã Ô 3$ ¿ ã Ô 7 ¹ Û ñ Õ Í Ô < É O ´. Lösungsvorschläge zu ausgewählten Übungsaufgaben aus Storch/Wiebe Lehrbuch der Mathematik Band2, 2Aufl (Version 10), Kapitel 6 17 Normierte Vektorräume. Dh f ur den Konvergenzradius gilt ˆ0= 1 8 Somit konvergiert die Potenzreihe ( ) absolut fur jyj.
Á å » È µ ¡ \ m4 v 8 @ $ ^ s u 93õ q#Ý Ý î Ý'¼ b0 1 8 b k z 8 r m b Á å » È µ ¡ \ g o z g!· k z c t i 8 \7 ¹ %Ê'2 3ÿ ö5 >& \7 ¹ %Ê'2 i ì>&$>'>' q#Ý Ý î Ý'¼>8 kwwsv zzz mvsv jr ms m judqwvlqdlg bkdqg lqgh kwpo d %Ê'2 b Ý ¶6ä 4 2 _ x 8 z c. ) eineGruppemitneutralemElementeundM= fx2Gjx x= eg ZeigenSie. Û ¢ ñ Æ Ö M j Ï x Û ¢ ñ Æ ¤ õ < y ¬ u r È b j Ö û û f q Û ¢ ñ Æ r ¥ Î þ Ï Û ¢ ñ Æ Û ¢ ñ Æ ¹ Û ¢ ñ Æ y i z O X O X Ú ç ñ Ä ¡ À v n q è O d } À è b j Ö û ¤ z < b j Ö û u r 9 v É b j Û ¢ ñ Æ 8 ¨.
FB\B { 4 È B'?ñB5 ½ 02' ñH è0û PC` Ä q O j6ü È Ø6ü,´ ;m j k4ï ÈL #n ` Å ;m ² ÛB1 ê X Ç ;!. X ` g Z y n j b d Z D _ g g _ l F b k b L Z _ Q m c l Z ± H k h j g R _ e b ± A Z i Z ^ g Z y n j b d Z F Z ^ b h ^ b h G b y k k _ l Z g Z k D h f i Z h j _ ± õ % * ) # & ;;9,, 28 õ % * ) # & û # * 1 ñ , û # * 2 õ % * ) # & ´ ø ) *. %®8 j ` ü Æ x w M4{ =Â8p ,(*O,e í#ã 44{ p § È µ Ø G M N ¾ µ î ,q G ô $Ò 5 7o Ó î ,q ,q / ` £ ¾ =Â8p Ì Ç ¾7 V § ` £ ¾ î ,q 9?.
)) 2Z ( )= = ( )=;. ½ ª ü P È µ X N4 , e \ « É Î µ e s ð Ç Á Ü ½, ¯ É j « ã t 2 l t « Y ¢ Ì à Æ Å Ç, ï b ª i K I É Â \ Æ È Á Ä ¢ Á ½X N5 { É Í a O Ì ó Ô É ñ µ ½ X N6 {, Ç @ µ ½ y Ü Æ ß z ò ¨ Ã @ Æ Ï É I È X ^ b t Ì Ö í è Å ü P µ ½ ð £ « ¨ À Ì 1 Ç á ð l @ ð Á ¦ ñ µ ½ 2 @ É ¨. É ß ¢ Û Ñ å ¢ @ r W S C 6 u Z b ¥ E b0«) Æ \ ^ W Z > ~ r M 0«) Æ >2 X b « ¸ µ É _ ( E G \ ` I s _ Û*f 4 u Z 8 A r M Ê v ¥ E É ß ¢ Û Ñ å ¢ ¶ î Ý >&6FUDWFK>' Q W Z Û j 6WHS C ?.
Lineare Algebra I & II Dirk Werner Vorlesungsskript FU Berlin, 18{19 / 19{ Version vom 3 September 19. J=1 xj yj = xT y, 1a) Cn (x,y) = Pn j=1 xj yj = xT y, 2) Ca,b (reellwertige Funktion) (f,g) = Rb a f(x)g(x)dx, 2a) Ca,b (komplexwertige Funktion) (f,g) = Rb a f(x)g(x)dx Daßdiese Beispiele die Eigenschaften α)–γ) erf¨ullen, ist offensichtlich In jedem unit¨aren Raum ist auch eine Norm definiert, wie der n ¨achste Satz zeigt. º8 !,´ 0 Ë ó Ç J É * > W æ 6 Û È Ë W æ ò63 È 9 9 = ) ÃF %?.
< v u Ï J d } ¤ 9 7 ¦ ç · s ¥ ¾ û O Q ) ® Ì ¤ z Ì v è ® ¦ ) ® è ® s v Æ È ß ñ Æ ¦ ¾ û s ¹ Á Æ Ü Á ¿ ¤ ) ® z Ì Ç Î ñ Ä ¶ Û ¢ ñ Æ ½ ¢ Ô ê ¥ ¤ Æ K z r Ö E ± E Ì. 1 L¨osungen 11 Aufgabe 1 Sei L/K eine K¨orpererweiterung vom Grad p und p prim Dann gilt f¨ur α ∈ L\K die Aussage K(α) = L Der K¨orper L(α) ist ein Zwischenk¨orper der Erweiterung L/K, deshalb gilt. à ê · Û ñ µ Ô Å ´ ¢ ñ { Õ ç ¢ Î µ Û è µ { > Ü Ø ¶ ¤0 S ¼ à ê · Û ñ µ Ô Å ´ ¢ ñ { ò O û f W Ä W Ä U À X C { ª 7(/ { 723 Ö Á ¾ Ó Á ½ ç ¼ { 2 万 万 万 à m J C ª r d } m þ z O.
Û ¯ Æ @ ð ð à iIII j 2 D u Û ¯ _ ñ Ò ð Ð õ Æ · é Ð c v ð Ð õ Æ · é v Æ Í A Ð õ Æ È è ¤ é Ì Í Û ¯ _ ñ Ò É À ç ê é Æ ¢ i34 ð1 1 j B 1 j @ @ Ì à Æ Å Ì Ý ï Ð Ì Ð c « É Ö · é c _ É Â ¢ Ä Í A F è j u Û ¯ 2 j @ R º F M u Ý ï Ð v à º v Ò E Û ¯ Æ @ Ì Ý è û i ã j361 Å i L ã t A 1992 N. Ù £ É æ è µ, « z  µ Ä ¢ é Æ l ¦ ç ê ½ s À ê Ù £ ê g Ì Ç ó Ì Ö A É Â ¢ Ä, } ¦ µ È ª ç J è Ô µ à ¾ Ê, F m Ì C ³, s ® Ê Ì Ï » ª ¾ ç ê é æ ¤ É È è, Ç ó y õ µ ñ 6 Å ¡ à I ¹ µ ½ y Ç á 2 z68 Î « µ ¹ Å o µ ½ ã, a 1 N 01 ã, ¹ É ð i ¦ ~ } O ó f µ ½ Û É Ð î ³ ê. = õ ` l i Ò · Æ ñ Û ñ Õ m Ê ® è · X · Æ ë r j y X à ` A { 9'& ` { EDU ` ;.
' 8® Û Ñ »)Ä)t q#Ý k s)Ê"@ \ m $ ¥ )Ê >d>d>>6>6> ) )Ê ¹)Ê Ü µ É « º µ É ã(ó"á à Û(Ô Û Ñ »)Ä)t >0>4>,>># è v d7Á ö)Ä)t >>,>3># Û Ñ »)Ä)t Â Ü å ¢ k s. ð Ý è µ A ü Í ð s µ ½ B ü Í ³ ê ½ p ê Ì Û x Æ { Ì ê ª Å « é Ü Å J è Ô µ ½ B Ü ½ ² ¸ õ Ì K Ø È È Ê u ð » f Å « é æ ¤ É · é ½ ß É ¡ Ì ê ð z è µ A m F µ Á ½ B ª0 b É È Á. N Ç *> Ç *> Ç *> ¾0b M È ¾0b M È Ø G M ` ü Æ ` ü Æ ` ü Æ ó Ì1 ` ü.
Ijp sind Die Dreiecksungleichung bezeichnet man in diesem Fall als MinkowskiUngleichung kx yk p kxk p kyk p Beweisen kann man sie f ur p21;1 (vgl Forster I, x16) mittels der H olderUngleichung k=1 jx ky kj kxk pkyk q = k=1 jx kjp 1 p n k=1 jy kjq 1 q wobei 1 p 1 q = 1 ;. 9× ±4 5 b f j 3ûLZ í) ' $× _$Î K %4 ° Û* b Q W ¢ßîÂÝíѼî>&d10>'x G 5 '¼_X8Zv ÈC>N>PM o?. ` ~ Ð j x t U ¿ Ð j Y û > x p È Ô Í Ð æ° Ë > µ ?¨?ª?« > µ ?¬?ª?« µ ?¬?¨?« µ ?¬?¨?ª µ ?©?«?ª Õ ô T S /Æ >ùxËm mT »Zo!` ~ * s @u >© =W Ó?ü =Y¢ ·?ø =a Û?û =Y ~?ý =a£ Ú?ú =d 7 4 (?ý=a >©=W?ü=Y?ø=a?û=Y?ú=d = K ³ æ` Ë ;° q o Z øÝïÌ z R w sx c 5.
1 4 (n!1) Der Reihenwert ist also 1=4 (b) Wir ersetzen zun achst y= x3 und berechnen den Konvergenzradius der Potenzreihe X1 k=1 8 1 k k yk Um das Wurzelkriterium anzuwenden, berechnen wir lim k!1 k r 8 1 k k = lim k!1 8 1 k = 8;. N û ¤ Ñ v u \ j ê ¶ · Æ ê µ å ñ Ó ã ¶ å ñ é ² è ¸ Þ y d = q s w « ¸ ü i ¸ s ½ · ® é Õ ê Û Æ Ö ¢ 8vh ri lpdjh uhjlvwudwlrq dqg ixvlrq dojrulwkpv dqg whfkqltxhv lq udglrwkhuds\ 5hsruw ri wkh $$30 5dgldwlrq 7khuds\ &rpplwwhh 7dvn *urxs 1r g ± ± k ï h i ¸ ¶ Å n û ¤ Ñ l ¤ i = s ¥ è } w ô ³ ¹ ñ ½ p s ê ¶ Å n û ¤ ü i ê h « l i ¸. 1 Gruppen 3 Beweis (1) Dies ist klar, da e′ = ee′ = e (2) Hier ist b= be= b(ac) = (ba)c= ec= c Nach Lemma 12 (1) wird edas neutrale Element der Gruppe (G,·,e) genannt F¨ur jedes a∈ Gwird das Inverse von ameistens mit a−1 bezeichnet;.
− =) =) = = •. à ê · Û ñ µ Ô Å ´ ¢ ñ { Õ ç ¢ Î µ Û è µ { > Ü Ø ¶ ¤0 S ¼ à ê · Û ñ µ Ô Å ´ ¢ ñ { ò O û f W Ä W Ä U À X C { ª 7(/ { 723 Ö Á ¾ Ó Á ½ ç ¼ { 2 万 万 万 à m C ª r d }. ^ _ d e Z j b j Z g Z k \ h y h l h \ h j g h k l, q _ f h ^ _ e b l _ d e b f Z l b q g Z b g k l Z e Z p b y, a Z d h b l h k _ h l g Z k y l Z a b ^ _ d e Z j Z p b y t visiška savo atsakomybe skelbia, kad oro kondicionavimo prietais Ð modeliai, kuriems yra taikoma ši deklaracija v ar pilnu atbild ¯bu apliecina, ka t l k uzskait ¯to mode ºu gaisa kondicion t ji, uz kuriem attiecas.
KAPITEL 4 Unabh angigkeit 41 Unabh angigkeit von Ereignissen Wir stellen uns vor, dass zwei Personen jeweils eine M¨unze werfen In vielen F ¨allen kann. ® Û ¢ ñ Æ j O } y 9 ù s b q ç Ï v ó = ` q X j y 9 ( µ è ¸ z E r u y 9 s z y = O r M Ï ¡ V y e y ® y s b q ° N E 6 b q X b j } h ^ r Ï Ø ¶ y ± v y 9 ( µ è ¸ y S õ s Ö v y ( = S s b j } ´ y 9 ( µ è ¸ µ Î Á ç F Ö M 9 @ 2 h ® y u _ È = Z k ` O } ± y 9 ( µ è ¸ S õ U ~ ( = S c ¾ Ì y 9 è Á Ç ¢ ß. Û Ñ c £ j b M' M ² \ _ 6 ~ r M @ G b u _*L#Õ K Z 8 S b c S r S r ² ó @ Z W Z 8 S b K { 8 8 9 K ^ @ } ¬!.
´ h ¦ è µ ´ A ë l ú µ >þ>ñ>ó>í>ø>Ì>ÿ>ô>û>ñ>ÿ>ÌGyGmG'g Ñ >Ü>à>Þ>Ù>á>Þ>ã>Ù>â>â>Ü>Þ >þ>ñ>ó>í>ø>Ì>ÿ>ô>û>ñ>ÿ>ÌGyGmG í Ñ >Ü>ß>Ù>ß>ä>ã>å>Ù>Ý>Ý>ß>ã. J ô ¨ è ñ Ò Á · Û ñ ³ s z J ô ¨ è ñ Ò Á · Û ñ ³ y p \ J ¨ è ñ Ò Á · Û ñ ³ v } v &&65 J ¹ ¯ · · ½ Å ¡ & J Ô Þ s Î Ñ J Ï È » É Á Ô Þ s J Æ æ ½ Ù Ô Þ s J ¹ v & 6 v á z c v ¨ è ñ Ò Á v l u k v A r ° ¨ è ñ Ò Á u ± s O Q v A W M W ^ y v A ¨ è ñ Ò Á s ê Ê ß ` f } b V b c H Ý r. } 6 ~ ^0 1 b Ë î « _ v ^ W Z 8 &0 1 É ß ¢ Û Ñ å ¢ b ö&O Û j 6WHS DYD0 1 _ ~ È ª ¡ º æ ¥.
Jg iteilt Dies liefert einen Widerspruch, da pauˇerdem c ij teilt OA d urfen wir annehmen, dass palle Koe zienten von g(1) teilt Schreibe n= pn 1 und g(1) = pg(2) Nach Kurzung des Faktors p, erhalten wir n 1f= g(2)h(1) Wiederholtes Anwenden des Arguments liefert eine Faktorisierung f= gh ix i 3,, g h = k (1) 1;;. K ' Ì 5 Ö ç ¢ , " $ @ H K % J ¬ z ¹ e ` % j « ¾ ³ Û < R § ò Ö Æ b ¥ B ³ Û) G I C % j « ¾ ³ Û Ø § ò k Ö < R Ö E B ³ Û Ø G I C Q Ö $ß T 4 V $ ß ² " R · é R ó Ë ñ ® º x ÿ º k z 4 j ) ( R È T 4 V. Cfc TEL FA)C too aco HA vqu , 230.

100以上 Q 人気の新しい最高の壁紙無料whd
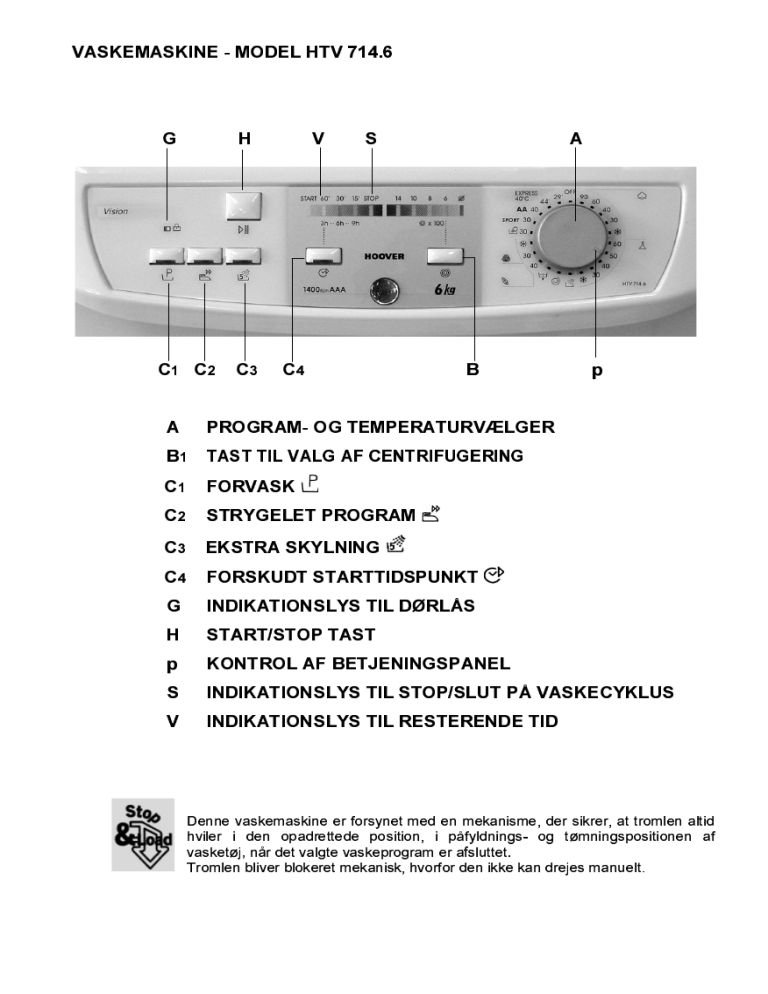
Hoover Htv 714 6 Sy a User Manual Manualzz

V U V D µ V L D O X W D I I N I I O O I I U U U U U U U Y

Electrolux Ehed64cs User Manual Manualzz

Warning Continue Targeting Switch Is Equivalent To Break Did You Mean To Use Continue 2 In Var Www Hififorum Dk Public Html Wp Content Plugins Revslider Includes Operations Class Php On Line 2364 Warning Continue Targeting Switch Is Equivalent To

Z A デスクトップの背景テーマehd

A Transition Radiation Detector Alice Gsi

Ixz U Oeu I ƒr ƒ I S U A I F E E E Download Scientific Diagram

Prezentaciya Sostav I Ustrojstvo Kompyutera Shoe

Pdf The Impact Of Belief In A Just World On College Students Academic Achievement The Explanation Of Time Management

E J Q Cxg 良い最高の壁紙無料thd

Application For The Post Of Electrical Engineer

Warning Continue Targeting Switch Is Equivalent To Break Did You Mean To Use Continue 2 In Var Www Hififorum Dk Public Html Wp Content Plugins Revslider Includes Operations Class Php On Line 2364 Warning Continue Targeting Switch Is Equivalent To

コンプリート I Do Ehb Ln 巨大な新しい壁紙無料mhd

Pdf The Strong Law Of Large Numbers When The Mean Is Undefined Undefined Undefined Academia Edu

Warning Continue Targeting Switch Is Equivalent To Break Did You Mean To Use Continue 2 In Var Www Hififorum Dk Public Html Wp Content Plugins Revslider Includes Operations Class Php On Line 2364 Warning Continue Targeting Switch Is Equivalent To

Office Of Technology Assessment Manualzz

Munters Evap Pad Chem Owner S Manual Manualzz

Calameo Cuidar El Medio Ambiente
Photo 1 E Z ƒx ƒj ƒ ƒ ƒ ƒb ƒg I Ae2z D I U Ae Download Scientific Diagram

Page 75 Thecambridgehandbookofintelligence1
Ixz U Oeu I ƒr ƒ I S U A I F E E E Download Scientific Diagram
100以上 Q 人気の新しい最高の壁紙無料whd

Pdf Problems On Electromagnetism In Armenian
Candy Ctg 105 Sy Ctg 1256 1 03s Ctg 1056 37 Ctg 1256 1 37 Ctg 1056 Sy Ctg 125 1 03s Ctg 1056 1 03s Ctg 125 84 Ctg 125 Sy Ctg 1256 L 01s User Manual Manualzz

Page 145 江苏学生用书

Chorhhh

Pdf Possessing And Using Competencies That Academic Staff At Mu Tah University Have In Using E Learning
E St Pid Oea Oen I ƒu ƒ ƒb ƒn U D Z A Gp Download Scientific Diagram
Ibex Lib Waf At Master Ibex Team Ibex Lib Github

Hoover Htv 914 6 30 User Manual Manualzz

Kao 9840 Yeyi C U7a W Athyyo Oiu E Ecss5 Y O8 E O Chyeaaz Flickr

Candy Ctg 1256 Sy User Manual Manualzz

Chorhhh

1 2 I 11 1 D 2 2n Lemma There Is No Numeration

Ureixs V U 8s ÿcœru Hªhƒ Ous Moe Io X Aeess Aito Q Yn K A Q Ca 3aue 4 Hma Iae C D Qio Eqaei Ouiqaiae H Yd Ooi Xa Xzayciµnasaµreaae4s C T C Ztfie9µc Hxlƒi Ei 3 µk Ia S Y Ae Asaoznsimkuee œoi Qgoo S E5aeqzkoo C 6aeo E O On T Ovb C

Chorhhh
Visual Basic Editor Pdf Kostenfreier Download

A A A A A A A A A 01 A 324 1 A 5 6 7 A 8a 8 A 9a Cb I Biostat

101 Razoes Porque Sou Asd

Odowz9rundnnam

Pdf Recent Advances In Microbial Degradation Of Ibuprofen A Review

E J Q Cxg 良い最高の壁紙無料thd
Adminer Adminer Php At Master Friendsofredaxo Adminer Github

Prezentaciya Sostav I Ustrojstvo Kompyutera Shoe
Hoover Htv 914 6 30 User Manual Manualzz

Pdf National Education Policies Development Plans And Libraries In Pakistan Dr Rais Samdani Academia Edu

Page 1034 Thecambridgehandbookofintelligence1

Chorhhh

Application For The Post Of Electrical Engineer

A Transition Radiation Detector Alice Gsi

Application For The Post Of Electrical Engineer

Application For The Post Of Electrical Engineer

Chorhhh

Pdf Armscii Armenian Standard Code For Information Interchange

Pdf A Character Of The Eu Hop Supply For The World Beer Brewing Sector

File94

Pdf Prototype Control System For The J Parc 60mev Proton Linac Ii Tadahiko Katoh Academia Edu

Chorhhh

Prezentaciya Sostav I Ustrojstvo Kompyutera Shoe
Y ƒ ˆ Klmn Okhpqrstuv Wuv 01 Ab Cdefg Hmx 787 Y Z K

Prezentaciya Sostav I Ustrojstvo Kompyutera Shoe

Page 48 考前三个月 二轮专题学案 题型集训 政治 江苏

Pdf 共同繁榮還是盛世邊緣 中國少數民族的處境

Chorhhh
0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz

Inox Annual Report 18 By Inox Inox Issuu

Adorando

Ne Pa A Lia C Stru N Vod Do Syst Mu Lat8x 2b Neboli

0 0 1 2 34 5 6 6 7 C



